انحراف معیار (standard deviation) در بازارهای مالی چیست؟

فعالیت در بازارهای مالی برای معامله‌گران، همراه با قبول ریسک‌های اختصاصی آن بازار است که بخش زیادی از آن‌ها به صورت غیر سیستماتیک اعمال می‌شود. یکی از راهکاری‌هایی که معامله‌گران حرفه‌ای برای کاهش زیان‌‌ در بازارها دنبال می‌کنند، استفاده از روشی است که بتواند ریسک‌‌های غیر سیستماتیک یا معاملاتی آن‌ها را به حداقل رسانده و متناسب با آن سطح از ریسک انتخابی، بالاترین بازدهی را نصیبشان کند.

در ادبیات مرسوم تحلیل ریسک، روش‌های متفاوت و متنوعی برای اندازه‌گیری میزان ریسک موجود در یک دارایی وجود دارد. یکی از اولین روش‌های متداول مورد استفاده معامله‌گران، بهره‌گیری از انحراف معیار(Standard Deviation) است که می‌تواند به عنوان یک نشانگر نوسان(volatility) عمل کند. 

انحراف معیار(standard deviation) چیست؟

انحراف معیار(σ) یک شاخص‌ پراکندگی در علم آمار است که پراکندگی مجموعه‌ای از داده را نسبت به میانگین() آن اندازه‌گیری می‌کند. این معیار به صورت جذر واریانس از طریق اندازه‌گیری انحراف هر نقطه‌ای از داده نسبت به میانگین محاسبه می‌شود. 

مقدار کم(کوچک) انحراف معیار نشان می‌دهد که داده‌ها در نزدیکی میانگین پراکنده شده‌اند و انحراف معیار با مقدار زیاد، نشان‌دهنده پراکندگی بیشتر داده‌ها است. همچنین انحراف نزدیک به صفر نشان می‌دهد که داده‌ها بسیار نزدیک به میانگین هستند، در حالی که انحراف معیار بزرگتر نشان می‌دهد که داده‌ها دورتر از میانگین پراکنده شده‌اند.

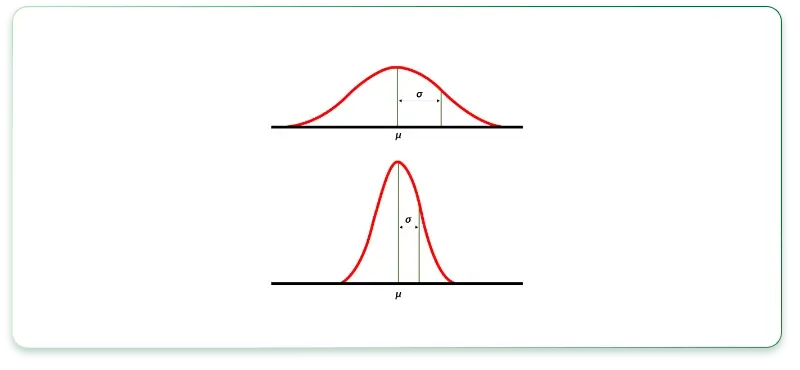
همانطور که در شکل زیر قابل مشاهده است، منحنی بالا پهن‌تر است و بنابراین مقدار انحراف معیار بیشتری دارد. اما در منحنی پایین، مقدار انحراف معیار کمتر است و پراکندگی داده‌ها در نزدیکی میانگین قرار دارد.

نحوه محاسبه انحراف معیار چگونه است؟

برای محاسبه انحراف معیار از رابطه زیر استفاده می‌شود:

در این رابطه، σ انحراف معیار است، xi هر مقدار موجود در مجموعه داده‌ها، µ میانگین و N تعداد داده‌ها است.

• ابتدا میانگین کل داده‌ها را محاسبه می‌کنیم.
• به فرض اگر ده عدد داده داشته باشیم، ابتدا داده اول را از میانگین کم کرده سپس به توان می‌رسانیم. این کار را برای کل داده‌ها انجام داده و نتایج را جمع(Σ) می‌کنیم. 
• سپس نتایج را بر تعداد مشاهدات(n-1) تقسیم می‌کنیم.
• در آخر جذر کل نتایج را محاسبه می‌کنیم.

همانطور که مشخص است، در معادله‌ی بالا، ابتدا واریانس محاسبه شده و سپس از آن جذر گرفته می‌شود تا انحراف معیار بدست آید. در حقیقت انحراف معیار جذر واریانس است. 

انحراف معیار در بازارهای مالی چیست؟

طبق مطالب بیان شده، انحراف معیار نشانگر میزان پراکندگی داده‌ها در اطراف میانگین است. از این رو اگر معیاری مانند «قیمت یک دارایی» یا «بازده» آن را داشته باشیم، با بدست آوردن میزان انحراف معیار آن داده‌ها، می‌توانیم متوجه میزان پراکندگی داده‌ها در اطراف میانگین شده و از این طریق، دید مناسبی از میزان تغییرات قیمت یا بازده آن دارایی در اطراف میانگینش بدست آوریم.

هرچه میزان این انحراف بیشتر باشد، بیانگر وجود «نوسانات» بیشتر در قیمت یا بازده آن دارایی است. 

محاسبه انحراف معیار برای دو دارایی در بازار سرمایه

برای اینکه بتوانیم میزان انحراف معیار را برای بازدهی یک دارایی در بورس اوراق بهادار تهران بدست آوریم ابتدا نیازمند جمع آوری داده از این بازار هستیم. در ادامه به هر نحوی که مایل هستید، داده‌های مربوط به یک یا چند نماد را جمع آوری کرده و بازدهی‌ را برای بازه زمانی مشخصی محاسبه کنید. 

اگر آشنایی کافی با دریافت اطلاعات از سایت شركت مديريت فناوري بورس تهران، ندارید برای مثال می‌توانید برای دریافت اطلاعات نماد «فولاد» به صفحه این نماد در سایت TSETMC  مراجعه کرده، وارد تب سابقه شده و از منوی «تهیه خروجی» واقع در بالا و سمت چپ جدول، خروجی بگیرید.

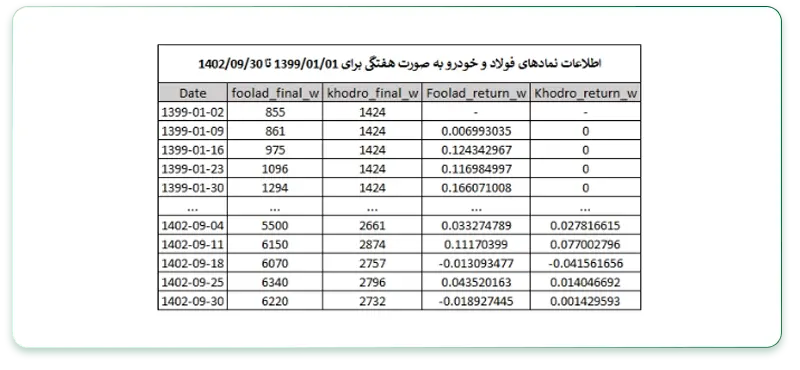
در ادامه از دیتاهای دو نماد «فولاد» و «خودرو» استفاده کرده و اطلاعات مربوطه را از سایت «tsetmc.com» دریافت کرده‌ایم. اطلاعات به صورت هفتگی و برای بازه زمانی 1399/01/01 تا 1402/09/30 است.

ستون‌های « final_w » بیانگر دیتای قیمت پایانی نماد‌ها در آن هفته و ستون‌های « return_w » مربوط به بازدهی لگاریتمی آن نماد است (بازدهی صفر بدلیل بسته بودن نماد معاملاتی در آن روزها است).

بعد از تکمیل این اطلاعات و ساختن دیتا فریم، حال می‌توان بر طبق فرمول گفته شده عمل کرد تا میزان انحراف معیار برای هر کدام از نمادهای نام برده را محاسبه نمود.

ابتدا میانگین بازده‌ها برای هر دارایی را محاسبه نموده، سپس مقدار مربع تفاضل هر داده از میانگین را محاسبه کرده و بر n تقسیم می‌کنیم که n برابر با تعداد داده‌هاست. در آخر هم مجذور مقدار بدست آمده را محاسبه می‌کنیم.

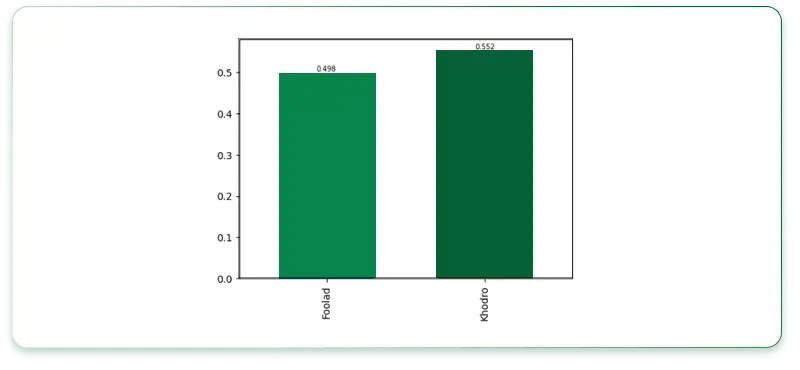
این مقدار برای نماد «فولاد» برابر است با «0.498» و برای نماد «خودرو» برابر است با «0.552».

همانطور که از خروجی شاخص انحراف معیار مشخص است، میزان انحراف معیار برای نماد «خودرو» بیشتر از نماد «فولاد» است که این شاخص به این معناست که داده‌های بازده برای نماد خودرو دارای پراکندگی بیشتری نسبت به میانگین بوده است.

سهامدارانی که نماد معاملاتی خودرو را برای سرمایه‌گذاری در این بازه زمانی انتخاب کرده‌اند، نسبت به سهامداران نماد فولاد، به صورت سالانه به مراتب نوسانات بیشتری را در بازدهی تجربه نموده‌اند. در نتیجه بر اساس معیارهای ریسک، این سهامداران در معرض ریسک بیشتری قرار داشته‌اند.

برای آشنایی بیشتر با مفهوم ریسک در سرمایه‌گذاری و شناخت ابعاد مختلف آن، می‌توانید مقاله «مفهوم ریسک و بازده در سرمایه‌گذاری» را در سایت آموزین مطالعه کنید.

در عمل برای معامله‌گرانی که در یک بازار مالی، سرمایه‌گذاری بلند مدت انجام می‌دهند، می‌تواند نگهداری سهامی در پرتفولیو دارای اهمیت باشد که بازدهی معقولی را با نوسانات قیمتی پایین‌تر محقق کند. از این رو استفاده از این شاخص در کنار شاخص‌های دیگر، می‌تواند به کاهش ریسک پرتفولیو سرمایه‌گذاری اشخاص کمک کند.

محاسبات با پایتون

اگر از زبان برنامه نویسی پایتون برای انجام محاسبات انحراف معیار استفاده می‌کنید، می‌توانید بعد از دریافت دیتا و محاسبه میزان بازدهی هر نماد، برای سهولت در انجام کار از کتابخانه قدرتمند NumPy  و دستور زیر استفاده کنید:

numpy.std(a, axis=None, dtype=None, out=None, ddof=0, keepdims=<no value>, *, where=<no value>)

در این عبارت، پارامتر a یک آرایه(array) می‌باشد.

محاسبات در اکسل

اگر از نرم افزار اکسل برای محاسبات خود استفاده می‌کنید، می‌توانید بعد از دریافت دیتا و محاسبه میزان بازدهی هر نماد، برای سهولت در انجام کار از تابع STDEV.S که در اکسل موجود است، برای محاسبه انحراف معیار استفاده کنید.

چه انحراف معیاری برای سرمایه‌گذاری مناسب است؟

انتخاب یک دارایی و سرمایه‌گذاری در آن، تابع فاکتورهای بسیار زیادی است برای مثال ممکن است یک معامله‌گر در مقطعی تصمیم بگیرد دارایی را انتخاب کند که از نوسانات بالاتری بهره‌ می‌برد، در نتیجه به سراغ دارایی با انحراف معیار بالاتر خواهد رفت تا در یک روند(صعودی)، بازدهی بالاتری نیز کسب کند.

همچنین ممکن است معامله‌گر، سایر شاخ‍ص‌های ریسک را مد نظر قرار داده و صرفا بر مبنای این شاخص و میزان آن عمل نکند. از این رو نمی‌توان پاسخ واحدی برای این سوال در نظر گرفت.

پیشنهاد مطالعه : <<آیا نوسانات بالای قیمت دارایی خوب است؟ >>

محدودیت‌های شاخص انحراف معیار

این شاخص نیز مانند بسیاری از شاخص‌های بازارهای مالی دچار محدودیت‌هایی است، به همین دلیل در گذر زمان توسعه‌یافته و به روز شده است. برخی از محدودیت‌های موجود به شرح زیر است:

• این شاخص گذشته‌نگر است و بر مبنای روندهای تغییرات قیمتی یک دارایی در گذشته خروجی می‌دهد، در صورتی‌که از نتایج آن برای پیش‌بینی عملکرد در آینده استفاده می‌شود!

برای مثال ممکن است یک دارایی مانند سهام شرکت تازه پذیرفته شده در بورس داشته باشیم که در زمان عرضه اولیه نوسانات زیادی داشته است، در نتیجه بر اساس اطلاعات خروجی شاخص انحراف معیار این دارایی، پر نوسان شناسایی شود اما به مرور با گسترش شرکت و رغبت بازار به این نماد، در آینده نوسانات کمتری را تجربه کند.

• داده‌های پرت که از میانگین فاصله زیادی دارند، تاثیر زیادی بر روی این شاخص می‌گذارند هرچند این داده‌ها پرتکرار نباشند.
• بسیاری از سری داده‌ها دارای توزیع نرمال نیستند و چولگی(skewness) دارند. از این رو خروجی شاخص انحراف معیار نمی‌تواند توضیح مناسبی از میزان پراکندگی داده‌ها در اطراف میانگین باشد.
• برای استفاده از این شاخص به عنوان یک شاخص ریسک باید به سراغ مدل‌های پیشرفته‌تری رفت یا آن را با در نظر گرفتن اطلاعات سایر شاخص‌های ریسک بررسی نمود.

پیشنهاد مطالعه : <<صندوق بخشی چیست؟>>

جمع بندی

در این مقاله تلاش شد شاخص آماری انحراف معیار و نحوه محاسبه‌ آن بیان گردد. سپس با استفاده از این شاخص به عنوان یک نشانگر نوسان در بازارهای مالی به بررسی یک مطالعه موردی در بازار سرمایه ایران برای دو نماد معاملاتی پرداخته و شاخص انحراف معیار(Standard Deviation) برای آن‌ها محاسبه شد.

همانطور که گفته شد، با محاسبه شاخص انحراف معیار برای نمادهای بورسی، می‌توان میزان وجود نوسان در چند نماد را بررسی و سپس متناسب با سطح ریسک پذیری و بازده دریافتی، اقدام به سرمایه‌گذاری در آن دارایی‌ها کرد. همچنین این نکته نباید فراموش شود که بهتر است از این معیار در کنار سایر معیارهای سنجش ریسک استفاده کرد. برای آموزش بورس میتوانید سایر مقالات آموزین را نیز مطالعه کنید.